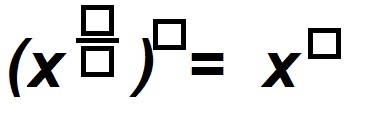Complex Number Operations- Open Middle Problem

Directions: Using the digits 1 to 9, fill in the boxes to make the equality true.  You can use each digit only once.

 

 

 

How does changing the signs between the Complex Numbers change the problem?

How does changing the signs between the Real and Imaginary parts of the Complex Number change the problem?

 

 

Properties of Powers- Open Middle Problem

Directions: Using the digits 1 to 9, fill in the boxes to make the equality true.  You can only use each digit once.

Can you write this expression in another way?

What is this defining?

Matrix Multiplication- Open Middle Problem

Directions: Using the digits 1-9, each only once, fill in the blanks to create the smallest possible value for a.

 

How would you change your numbers to create the smallest value for b?

Create matrices such that a and b are of equal value (if you can’t generate equal values, how close can they get?)

Creating Zero- Open Middle Problem

Using the numbers 1 to 9 at most once each time, fill in the blanks to make the equality true:

( ___ + ___ – ___ + ___ ) – ( ___ + ___ – ___ + ___ ) = 0

Absolute Value 2- Open Middle Problem

Using the numbers 1 to 9 at most once each time, fill in the blanks to make the equality true:

___ + ___ = | ___ – ___ |

Absolute Value- Open Middle Problem

Using the numbers 1 to 9 at most once each time, fill in the blanks to make the statement true:

___ and ___ are ___ units away from ___

 

Equal Tips- Open Middle Problem

Using the numbers 1 to 9 at most once each time, complete the following statement:

Leaving a ____ dollar tip for a bill of _____ is the same as leaving a ____ dollar tip for a bill of _____

What is the percent of your tip?

Which tip percentage has the most combinations given the set parameters?

Rational Numbers

Consider the Natural Numbers 1 to 9 for a and b.  When written in the form of a/b, what values for b always produce an irrational number (unless a=b)?

Graphing Roots

Consider the roots of the first nine counting numbers (√1, √2, √3, √4, etc).  Graph them on a 1:1 scale, 1:10 scale and 1:100 scaled number line.

 

 

 

What interval do these roots lie between?

 

Which interval was the easiest to graph on?  Explain.

 

Which scale would you use if you had to graph the next nine counting numbers?  Explain.

Operations with Rational Numbers- Open Middle Problem

Using Integers 2 to 9 (without repeating any number), fill in the boxes to create: