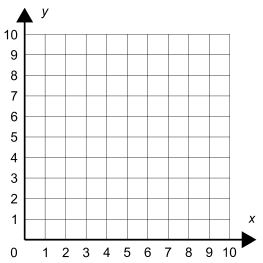
Directions: Using the following command blocks (at most one time each), create code that will place Scratch 2/3rd of the way along a line.
You may use the digits 0-9, at most one time each, to fill in the boxes to create your code.
If Scratch was 1/3rd of the way along the line, he would be at point ( ___ , ___ )
Note: we are making Scratch 30% of his size to see the line and proportion better
Directions: Create code that will make a regular polygon. You can only use command blocks once and the digits 0-9 once to fill each box.
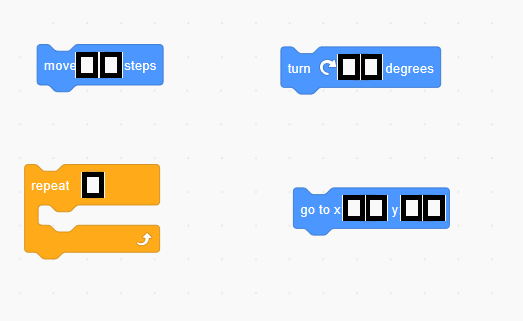The polygon this makes is a ____________________
Directions: Using the digits 0-9, no more than once each, fill in the boxes to make the statement true:
How would this problem change if it instead read:
Directions: Using the numbers 0 to 9, at most once each time, fill in blanks to create a set of 4 points that create either Parallel or Perpendicular lines, depending on how you connect them.
( ___, ___ ) ( ___, ___ ) ( ___, ___ ) ( ___, ___ )
Directions: Using the diagram, fill in the blanks with the names of the shapes to make each statement true.
__________ has more sides than __________
__________ has the same sides as __________
__________ has more vertices than __________
Note: you can choose to have students reuse shapes or use them only once.
Directions: Using the numbers 1 to 6, at most once each time, fill in boxes and identify a shape in the blank to make the following statements true.
Directions: Using the following picture, complete the following sentences (using the phrases: above, below, beside, in front of, behind, and next to)
The cube is ___________ the sphere and ___________ the triangle.
The hexagon is __________ the pentagon and __________ the circle.
Use the shape names to complete the following statements:
The ________ is next to the ________ and above the __________.
The ________ is beside the __________, above the ___________, and below the ___________.
Directions: Using the digits 1 to 9 and the math operations of +, -, ÷, ×; create expressions for the sides of the following pentagon where A > C > B.
What can you say about angles a and b?
What are the measures of a and b?
How do you know your answers are correct?
Are there any other solutions?
Directions: Using the following trig ratios, complete the following table:
cos 30º, sin 30º, cos 45º, sin 45º, tan 30º, cot 30º, sec 30º, csc 30º
What trig ratios CANNOT go in the center square?
What is the smallest trig ratio that can be placed in the center square?
Consider the following figure:
What values of x, y and z will produce the following inequality?
csc B < sec B < tan B < sin B < cot B < cos B
How does the inequality
sin B < tan B < cos B < cot B < csc B < sec B
change your diagram, values or thinking?
MathLab 