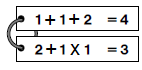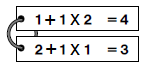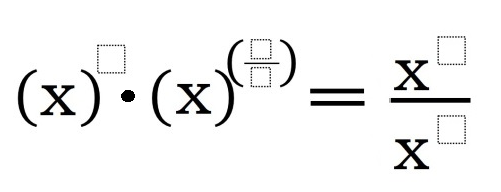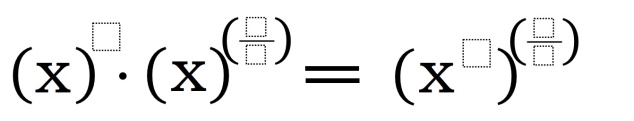Directions: Create code that will ask the user for a number and tell them it’s 10’s pair.
You can only use a command block once.
You can use the digits 0-5, at most once each.
Is there any code or numbers you did not use?
Code this in scratch and test it out, did anything happen that you didn’t expect?
What happens if you wanted to make 20’s partners?
Just for Christopher…
Directions: Using the numbers 1-6, fill in the boxes to make the following product true. You can repeat numbers as many times as you wish.
How many possibilities are there?
Explain your thinking to find your answer.
Directions: Using the numbers 1-9, each only once, fill in the boxes to make the following product true.
How many possibilities are there?
Explain your thinking to find your answer.
OK, the MTBoS has really influenced the way I approach teaching and assigning problems. Coming back from Christmas Break, I needed a different way to get students thinking about math again, and found that thanks to Math = Love in the form of Gemini Puzzles.
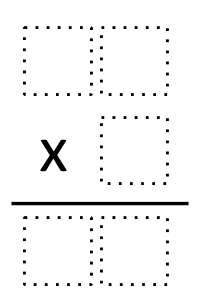
What are Gemini Puzzles? In short, they are equality statements that are missing any mathematical symbols. Here is an example:
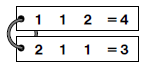
The thing I love about this is- I put these two on the whiteboard for students to see when they first walk in and instead of asking what we are doing today or talking about what they did last night, they started thinking about what was going on. The other great thing, I didn’t have to tell them what to do, they started playing around with the numbers to get it done.
When I asked my students what they were doing, there was a common theme:
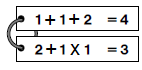
Which is great until I ask students about the name of the problem, Gemini. I then get answers about twins and I tell them that’s relevant to the problem. They are given two equivalence statements, and they have to be twins. In other words, anything they add to one statement has to be the exact same as what they add to the second.
Then students start working in a stream of consciousness and they have this as an answer:
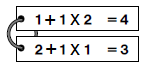
It doesn’t take too long for a student to say that there’s problem with this. Students are thinking “one plus one is two, times two is four”, but they are not properly showing that. Then the talk of Order of Operations hits, and students realize the first statement is only 3. By throwing in another set of symbols they find the correct solution:
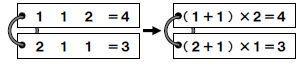
By providing students with two equivalence statements that need the exact same symbols to make them true, you are giving students a reason to think about the order of operations and how they interact. I have loved listening to student talk when working on these, and I even had students proudly come up to me with different solutions to a problem. They are amazed that there can be different ways to implement mathematical operations and get the same result (see if you can find which one they discovered!)
Gemini Puzzles are a great activity for the classroom, I know I’ll be using them from now on, I hope you enjoy them as well.
I currently have a range of students from 6th to 12th grade in my classes, with various mathematical skills ranging from 4th to 12th+, and these puzzles have engaged and challenged them all. It’s a great thing to see.
Directions: Using the integers 0 to 9, each only once, fill in the following blanks to make the equations true.
___ + ___ = 10 + ___
___ + ___ = 10 + ___
___ + ___ = 10+ ___
Directions: Using the Integers 0 to 9, each only once, how many different ways can you fill in the blanks to make the statement true?
Directions: Using the Integers 0 to 9, each only once, how many different ways can you fill in the blanks to make the statement true?
Directions: Using any number between 1 and 9, fill in the boxes to create a true statement. You may only use a number once.
If you could only use the numbers 1 to 9, each only once, could you fill in the boxes to make the figure true?
If not, explain why it doesn’t work. Where exactly in the table do you have problems? What is the smallest number of adjustments needed to make the table work?
Directions: Using any number between 1 and 9, fill in the boxes to create a true statement. You may only use a number once.
MathLab 