Directions: Using any number between 1 and 9, fill in the boxes to create a true statement. You may only use a number once.
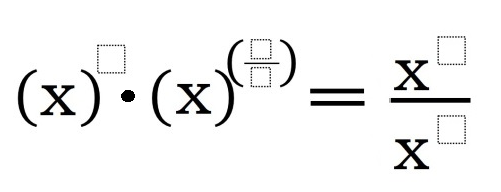

Directions: Using any number between 1 and 9, fill in the boxes to create a true statement. You may only use a number once.
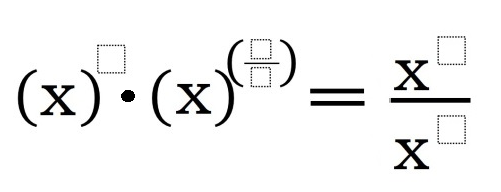
Directions: Using any number between 1 and 9, fill in the boxes to create a true statement. You may only use a number once.
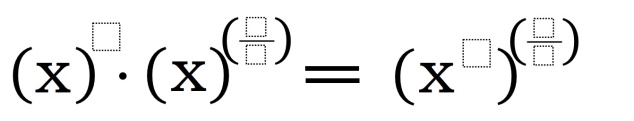
Act 1:
What questions do you have when you watch this video?
Ask students to write down their questions, I normally ask students to find at least 3. When I observe that most students have questions written, I ask them to share those questions with their neighbor. I then throw up a Microsoft Word document and start typing down questions students supply. Students from my classroom came up with all sorts of different questions, some we can easily answer and others that we can’t. I am looking for a key question or questions to start this lesson. If students do not ask one of these questions, I tell them that I hope I can answer most of the questions provided, but that I need them to consider one of these questions first.
Any of these type of questions will lead students down the inquiry I hope to explore with them.
How do you square binomials?
ACT 2:
Once again, this video can create a few different paths of exploration. We can explore:
These are both excellent topics and students generate a lot of classroom discourse discussing each one.
ACT 3:
Extensions:
Reflection:
ACT 1:
This video was inspired from comments made in Dan Meyer’s My Opening Keynote for CUE 2014.
What questions do you have when you watch this video?
Ask students to write down their questions, I normally ask students to find at least 3. When I observe that most students have questions written, I ask them to share those questions with their neighbor. I then throw up a Microsoft Word document and start typing down questions students supply. Students from my classroom came up with all sorts of different questions, some we can easily answer and others that we can’t. I am looking for a key question or questions to start this lesson. If students do not ask one of these questions, I tell them that I hope I can answer most of the questions provided, but that I need them to consider one of these questions first.
Any of these type of questions will lead students down the inquiry I hope to explore with them.
ACT 2:
Once again, this video can create a few different paths of exploration. We can explore:
These are both excellent topics and students generate a lot of classroom discourse discussing each one.
ACT 3:
Extensions: