Ordering Shapes- K,1
Directions:
Draw three shapes and order them from smallest to biggest.
Draw three more shapes and order them from biggest to smallest.
Look at your six shapes and order all of them from biggest to smallest.
Cube Numbering- Elem
How many different ways can you place the integers 1 to 6 on the net to create the cube pictured?


What are some things you know about dice cubes?
How does that effect your strategy for numbering?
How would this net change your strategies?

Or this?

Drawing and Naming Shapes by Sides- K
Draw and name a shape that has the following characteristics:
- Has 3 sides
- Has 4 sides
- Has 5 sides
- Has 6 sides
- Has no sides
Composite 2D shapes- 1st Grade
Directions: What shapes could be used to create this picture?
Make a list of the shapes needed, and how many of each you would need.
What other pictures could you make with these figures?
Shape Partitions- 3rd Grade
Directions: Using the same cuts, partition these shapes into halves.
Can you expand this to fourths? Explain why or why not.
Can you create fourths of each picture using unique partitions (no figure is partitioned the same)? Draw examples and explain why or why not.
Rectangle Construction- 3rd Grade
Directions: Using the following squares, how many different rectangles can you make?
How does adding 4 more squares change the problem?
Rectangle Partitions- 3rd Grade
Directions: Using the numbers 1 to 9, using each number only once, complete the following statement:
___ rows and ___ columns create a rectangle of ___ units
- What different possibilities will your students come up with?
- How many of these statements can you create?
- How would increasing the interval from 1 to 19 change the problem?
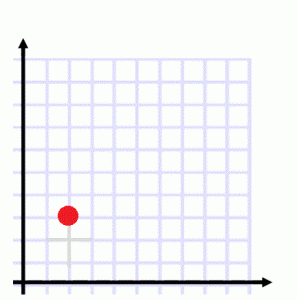
Creating Right Triangles- 8th Grade
Fill in the empty blanks so that you create a right triangle from the vertex (2,3). You can use whole numbers 1 through 9, but can only use a number once.
Creating Parallelograms- 8th Grade
Fill in the empty blanks so that you create a parallelogram from the vertex (2,3). You can use whole numbers 1 through 9, but can only use a number once.
( __ , __ ) ( __ , __ ) and ( __, __ )
Creating Rectangles- 8th Grade
Fill in the empty blanks so that you create a rectangle from the vertex (2,3). You can use whole numbers 1 through 9, but can only use a number once.
( __ , __ ) ( __ , __ ) and ( __, __ )
Tilings- 8th Grade
What is the least amount of Tranformations needed to Tile the plane? List them.
Can the tiling be done with only one type of Transformation? If so, identify which type and how many times you need to perform the transformation to tile the plane.
Will different orders of Transformations create different Tilings? If so, find out how many Tiling patterns are possible and list how to create them.
Transformations of a Point- 8th Grade
List the Transformations needed to map a -> a’ under the following conditions (all reflections and rotations will be through the origin):
If there are any you find that are impossible, identify them and why they can’t be done.
If you find an infinite number of possibilities, identify the pattern.
Transformations- 8th Grade
Transformations:
List 3 points that create a right triangle with an area of 6, staying within the axis provided below (-10 < x < 10, -10 < y < 10). Rotate your triangle and reflect it across an Axis. List the three new points.
Write down the steps you used to create your transformation.
Find another set of transformations that gives the same result as your original one.
(This can create a great number of variations: types of polygons, translations, reflections and rotations)
**This type of problem is a bit too open-ended for Open Middle, typically you strive to come to only one answer or a small set of correct answers, I purposefully left this problem a bit open-ended for my blog**
Parallelogram Proof- 8th Grade
Is this figure a parallelogram? Explain how you know.
Draw a diagonal of your parallelogram. Using 2 Transformations (Rotations, Reflections or Translations in any combination), explain how triangle 1 is congruent to triangle 2.
Alternate image for the same problem:
Right Triangle Similarity- HS
Directions: Using the numbers 1 to 9 and math operations of (+, -, x, ÷), how many different triangles can you create where tan Θ=.75?
Note: you can only use each number once per triangle created.
Trig Ratios- HS
Directions: Fill in the empty blanks so that you create a triangle whose Cos Θ = √2/2. You can use whole numbers 1 through 9, but can only use a number once: (5, 4), (__,__) and (__,__)
Trig Ratios- HS
Consider the following figure:
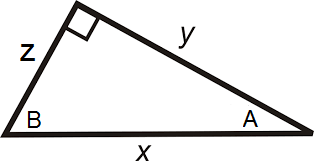
What values of x, y and z will produce the following inequality?
csc B < sec B < tan B < sin B < cot B < cos B
How does the inequality
sin B < tan B < cos B < cot B < csc B < sec B
change your diagram, values or thinking?