I love talking about OM problems, and when I do I always send the message that OM problems can fit into almost any aspect of your lesson- that you can decide when or where. I always assumed that people understood what I meant- now I realize I was being that teacher! I have had many people come to me after talks saying how they would like to know how I use it within my classroom. Before I forget to address this and give another presentation, I want to have an outline in my blog.
My daily routine typically looks like this: Bellwork -> Lesson ->Exit Reflection.
OK, this looks pretty simplistic, but I try to keep it that way. When I first started teaching, my school implemented the Developmental Design for Middle School and in their training, they had a lesson template that really connected to me for how I wanted my day to progress. I have been using the Origins Lesson Plan Template ever since (and each new Administrator asks me about it- but has always seen the value of it to me and my classroom). It looks like this:
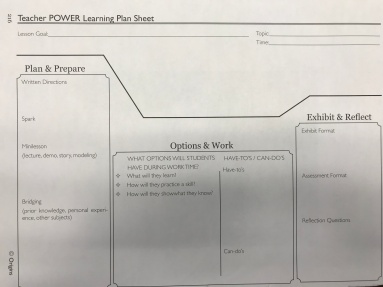
As you can see, even though I go through 3 transitions in my classroom, how they look and feel can vary. It gives my students the safety of knowing what the daily routine is, but give them the variety to keep things fresh, new, engaging. So my
Bellwork -> Lesson -> Exit Reflection translates to:
Plan & Prepare -> Options & Work -> Exhibit & Reflect on the lesson plan.
Now, in my talks I say that OM problems can be used at any point in this, so let’s look at how that could happen.
1) Bellwork OR Plan & Prepare
Everything I use in class has a purpose, it’s never time-filler. As such, I make sure to pick bellwork that will get students thinking of the upcoming lesson OR use concepts we talked about yesterday so that we can build upon them in the lesson for today. So one OM problem I like using for bellwork when we talk about functions in 8th grade is this:

I like this problem because even though it seems too open-ended, it can generate a lot of good discussions. Unlike a lot of other OM problems, it doesn’t provide students with a “fill in the box” format but it allows students to generate as many (or as little) points in the table as they want. I typically have students write their tables on the board and as a class we discuss whether they are a function or not. There are times I have DESMOS on the SMARTBoard and I enter the table when we are unsure. In 8th grade my students have an idea of what functions are or are not, and this sparks a lot of prior understanding and learning which primes them for the lesson.
2) Lesson OR Options & Work
I will keep with the functions theme through this example, but I will not use an OM problem more than once in any part of my day. It’s good to use them to challenge students, but if I am throwing too many/too often at students it looses its effectiveness. Let’s say I get done with a great lesson on functions and want to assign practice problems for students to explore, solidify and demonstrate their understanding. I do not believe in the “Do 1-60 odds” philosophy of homework, I did not benefit from this practice as a student and do not believe in it as a teacher. I do believe in providing students with a homework assignment that is manageable and have them thinking of math outside the classroom for 15-20 minutes of their day. As such, I like OM problems for this reason. Consider this problem:

Consider working on this problem as a 8th grade student. Will they get a lot of practice? How many problems were assigned? Do they know what rate of change is and how it effects the points that lie on the line? Will they have understanding of a function if they solve this problem? How can they demonstrate this? I believe they will have a solid understanding of functions and are ready to continue their learning of functions.
3) Exit Reflection OR Exibit & Reflect
I’ve had a great lesson on linear functions, and I am positive all of my students understand what we covered. How can I be sure? Well I give them an Exit Ticket OM problem to check that understanding and provide data for tomorrow’s lesson. remember when I had the OM bellwork to tell me what a function wasn’t? Well I could give them that problem again with a few more constraints (limited number set, minimum number of points, etc) or I could give them something like this:

I would like you to reflect on this. If your students can correctly answer this, was it a good learning experience?
Those are they ways OM problems would appear in my classroom, implemented in any of the 3 transitions of my classroom. I hope this helps you envision how you can use OM in your classroom to make homework problems more challenging and interesting.