Directions: Create code that will ask the user for a number and tell them it’s 10’s pair.
You can only use a command block once.
You can use the digits 0-5, at most once each.
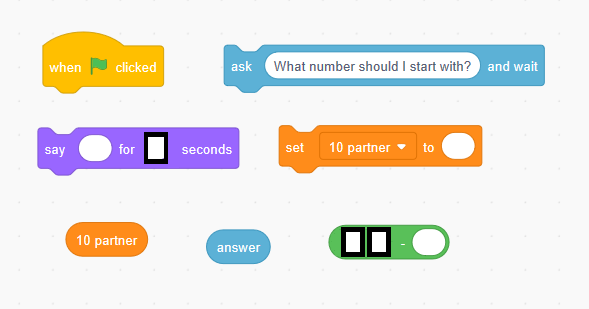
Is there any code or numbers you did not use?
Code this in scratch and test it out, did anything happen that you didn’t expect?
What happens if you wanted to make 20’s partners?
Directions: Using the integers 0 to 9, each only once, fill in the following blanks to make the equations true.
___ + ___ = 10 + ___
___ + ___ = 10 + ___
___ + ___ = 10+ ___
Directions: Using the Integers 0 to 9, each only once, how many different ways can you fill in the blanks to make the statement true?
Robert has 10 checkers. Checker colors are either red or black. How many red checkers and how many black checkers could Robert have?
What to you notice?
Is there a pattern?
Directions:
Draw three shapes and order them from smallest to biggest.
Draw three more shapes and order them from biggest to smallest.
Look at your six shapes and order all of them from biggest to smallest.
Using the numbers 1 to 6, using a number only once, create a graph and fill in the blanks to make them true.
There are ___ bananas, ___ apples and ___ oranges.
There are ___ more apples than bananas.
There are ___ less oranges than apples.
There are ___ more oranges than bananas.
NOTE: I would suggest having this pre-printed for students and have numbers 1 to 6 printed on paper that students can use as a manipulative.
Special thanks to @gfletchy for input on this problem and accomodations
Directions: Using the same cuts, partition these shapes into halves.
Can you expand this to fourths? Explain why or why not.
Can you create fourths of each picture using unique partitions (no figure is partitioned the same)? Draw examples and explain why or why not.
Directions: What shapes could be used to create this picture?
Make a list of the shapes needed, and how many of each you would need.
What other pictures could you make with these figures?
MathLab 