10’s Pairs – Open Middle Coding

Directions: Create code that will ask the user for a number and tell them it’s 10’s pair.

You can only use a command block once.

You can use the digits 0-5, at most once each.

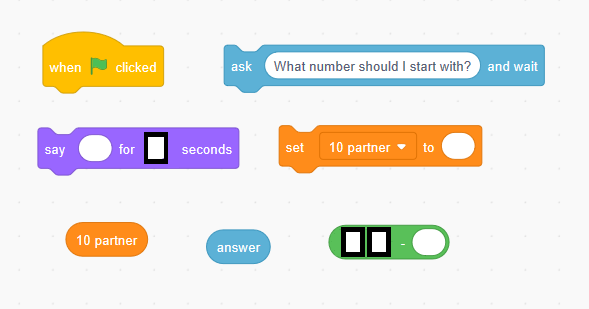
Is there any code or numbers you did not use?

Code this in scratch and test it out, did anything happen that you didn’t expect?

What happens if you wanted to make 20’s partners?

Analyzing Shapes- Open Middle Problem

Directions: Using the diagram, fill in the blanks with the names of the shapes to make each statement true.

__________ has more sides than __________

__________ has the same sides as __________

__________ has more vertices than __________

 

Note: you can choose to have students reuse shapes or use them only once.

Identifying Shapes- Open Middle Problem

Directions: Using the numbers 1 to 6, at most once each time, fill in boxes and identify a shape in the blank to make the following statements true.

Describing Shapes- Open Middle Problem

Directions: Using the following picture, complete the following sentences (using the phrases: above, below, beside, in front of, behind, and next to)

 

The cube is ___________ the sphere and ___________ the triangle.

The hexagon is __________ the pentagon and __________ the circle.

 

Use the shape names to complete the following statements:

The ________ is next to the ________ and above the __________.

The ________ is beside the __________, above the ___________, and below the ___________.

Comparing Numbers- Open Middle Problem

Directions: Using the numbers 1 to 9, each only once, fill in the blanks to make the inequality statements true.  The middle number of each inequality has to be odd.

the symbol < means “is less than”

 

EDIT: Thanks to Graham @gfletchy for talking this out with me- if symbols seem inappropriate for K, use the following:

___ is more than ___ but less than ___

___ is more than ___ but less than ___

___ is more than ___ but less than ___

Checker Combinations- Open Middle Problem

Robert has 10 checkers.  Checker colors are either red or black.  How many red checkers and how many black checkers could Robert have?

 

What to you notice?

Is there a pattern?

Drawing and Naming Shapes by Sides- Open Middle Problem

Draw and name a shape that has the following characteristics:

• Has 3 sides
• Has 4 sides
• Has 5 sides
• Has 6 sides
• Has no sides

Caterpillar Counting- Open Middle Problems

Directions: Fill in the missing numbers, then make spots on each body segment that represents the number above it.